La Energía de Fermi es la energía
del nivel más alto ocupado por un sistema cuántico a temperatura cero. Se
denota por EF y recibe su nombre del físico italiano-americano Enrico Fermi. La energía de Fermi es importante
a la hora de entender el comportamiento de partículas fermiónicas,
como por ejemplo los electrones. Los fermiones son partículas de spin
semientero que verifican el Principio de exclusión de Pauli que dicta que dos
fermiones no pueden ocupar simultáneamente el mismo estado cuántico. De esta
manera, cuando un sistema posee varios electrones, estos ocuparán niveles de energía
mayores a medida que los niveles inferiores se van llenando. La energía de
Fermi es un concepto que tiene muchas aplicaciones en la teoría del orbital, en
el comportamiento de los semiconductores y en la física del estado sólido en
general. Brevemente se puede decir que la superficie de Fermi divide los
estados electrónicos ocupados de los que permanecen libres [2].
Enrico Fermi y Paul Dirac,
derivaron las estadísticas de Fermi-Dirac. Estas estadísticas permiten predecir
el comportamiento de sistemas formados por un gran número de electrones,
especialmente en cuerpos sólidos.
Donde eF es la energía de Fermi, k es la constante de
Boltzmann y T es la temperatura. Por lo tanto, el potencial químico es
aproximadamente igual a la energía de Fermi a temperaturas muy inferiores a una
energía característica denominada Temperatura de Fermi, eF/k. Esta temperatura característica es del orden
de 105°K para un metal a una temperatura ambiente de (300 K), por lo que la
energía de Fermi y el potencial químico son esencialmente equivalentes. Este es
un detalle significativo dado que el potencial químico, y no la energía de
Fermi, es quien aparece en las estadísticas de Fermi-Dirac.
FUNCIÓN DE FERMI
La función de Fermi es una función probabilística, que indica la probabilidad de que un estado cuántico de energía E este ocupado por un electrón, también especifica la fracción de todos los estados de energía E ocupados en condiciones de equilibrio térmico [7].
 |
| Ecuación 3.1 |
Donde:
EF= Energía de Fermi
E=Energía
K= Constante de Boltzmann cuyo valor es K=8.62 x 10-5(eV/°K)
T= Temperatura
Para un gas ideal, si aplicamos la función de Fermi para un Temperatura T=0 y para E>EF teniendo la ecuación (3.1).
La ecuación 3.1 queda de la siguiente forma:
F
(E)= 0
Si aplicamos la función de Fermi para
un Temperatura T=0 y para E<EF
retomando la ecuación (3.1).
La función de Fermi es igual a uno para una Energía E mucho menor a EF.
F
(E)= 1
Para bajas temperaturas la función de Fermi es un escalón como se muestra en la figura 3.1, quiere decir que los electrones se van colocando desde el nivel más bajo de energía hacia arriba, hasta que se hayan puesto todos los electrones en orden.
F (E) = 1 cuando E < EF
F (E)= 0 cuando E > EF
 |
| Figura 3.1 Función de Fermi para T=0°K |
La grafica muestra que a 0°K los
electrones están a su nivel más bajo de energía. La probabilidad de que un
estado cuántico este ocupado es uno para
E<EF, y la probabilidad de que este ocupado es cero para E>EF.
Todos los electrones tienen
energías por debajo de la energía de Fermi a T=0°K.
Si aplicamos la función de Fermi
para una temperatura mayor a 0°K, de la ecuación (3.1) tenemos:
T>0°K y E=EF
Para este caso la
función de Fermi se expresa como la probabilidad de que un estado este o no
ocupado de 1/2.
La figura 3.2 muestra
la representación gráfica de la función de Fermi para T diferente de Cero.
Donde de acuerdo a la función de
Fermi se puede deducir lo siguiente:
Aplicamos a la ecuación (3.1)
Si E= EF+ KT
Si E= EF+2KT
Si E= EF+3KT
Se observa que todos los estados
que tienen una energía de 3KT por debajo de la energía de Fermi se considera
que están libres o desocupados, la probabilidad es por la función de Fermi de F (E)=0.474.
Ahora, aplicando a la ecuación
(3.1) Función de Fermi para:
E= EF- KT
E= EF- 2KT
E= EF- 3KT
Por arriba de 3KT del nivel de
Fermi todos los niveles energéticos tienen la probabilidad de F (E)=0.95 de estar ocupados [1].
Como puede verse si E = EF para todas
las curvas para T > 0 ºK pasan siempre por
F (E)=(E=EF) = 1/2. Para temperaturas mayores a T= 0 ºK hay una
probabilidad no nula que algunos estados de energía por encima de EF estén
ocupados por electrones y, consecuentemente, algunos estados por debajo de EF
estarán vacíos.
En resumen para un estado con energía E>Ef
tendrá más posibilidades de ser ocupado a mayor temperatura. A una temperatura
T, la probabilidad de ocupación disminuye si aumenta la energía. Para cualquier
T, la probabilidad de encontrar un electrón con una energía Ef es de 1/2.
A T=0 la probabilidad de encontrar un electrón con E>Ef es 0 y con E<Ef es 1.
Si la probabilidad de encontrar un electrón es f(E), la probabilidad de no encontrarlo (o tener huecos) es 1-f(E).
La imagen 3.3 muestra las curvas características de la función de Fermi para diferentes temperaturas y se puede observar las diferentes probabilidades de ocupación.
 |
| Figura 3.3 Curvas características de la función de Fermi |


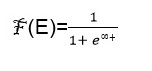










Comprendí muy bien todo. Gracias
ResponderBorrar